「トニーのおっさん」のリバプール語録vol.4：フォーメーションの3-3-3-1理論

この記事を書いた人
最新の記事

LFCラボ

リバプールFCラボの管理人です。

「トニーのおっさん」のリバプール語録とは？

僕はオフィシャルメンバー登録もしてるし、定期的にアンフィールドに赴き、オフィシャルショップの店員から「あなた世界で一番オフィシャルで使ってるわ」と言われるくらいグッズを買いまくるリバプールファンではあるが、地元のファンからすれば『外国人』だ。

— トニーのおっさん (@tonynoossan) 2015年11月6日

Twitter上でリバプールを様々な角度から分析し、その知識の深さから「この人は何者！？」とリバプールファンの間で騒がれている「トニーのおっさん」さん。ご本人にご協力をいただき、リバプールFCラボでは「トニーのおっさん」のツイートを不定期でまとめて記事コンテンツとしてデータベース化していきます。「移籍考察」「試合分析」「クラブ経営」「その他豆知識」など、リバプールの理解を深める数々の語録をご覧ください。

今回はトニーのおっさんによるサッカーのフォーメーションが行き着く3-3-3-1に関する見解をご紹介します。

3-3-3-1理論（以下ツイート引用）

初日のディナーで、マンチェスターシティーのアカデミーでのポジショナルプレーと、未来のサッカーが3-3-3-1になる理論と、フェルハイエンのピリオダイゼーションは現実主義的に作った物のはずなのに現実に使えなくなってきてる話になるって、何なんですかこの人たち。バケモノですかね。

— M. Hayashi (@Hayashi_BFC) 2018年3月20日

多分、ピッチを完全に均等にカバーする事を考えたらそうなると思う。

ポジションという概念が無くなると予想してんだと思う。ポジションを固定するというのはWMシステムのころからそうだけど、つまりはフォーメーションという陣形を組んだ方が勝てるという発想。それが進化し続けるうちに、固定された陣形よりも陣形から受けられる機能やメリットを享受しつつ、流動的に動く事で固定された陣形の脆いところを突かれるデメリットを消すという発想に行き着くんだと思う。

完全に性能が同じロボットでフットボールをする事になれば、フォーメーションは3-3-3-1になるのかもしれない。フットボールではなく11vs11で棒持って殴り合うって考えてるのかもしれない。思考の根底部分で。

単純なフラットの4-4-2だと選手間のパスコースを図形の辺として考えると21辺になる。21辺だよな？多分。一応数えたけど、21辺。

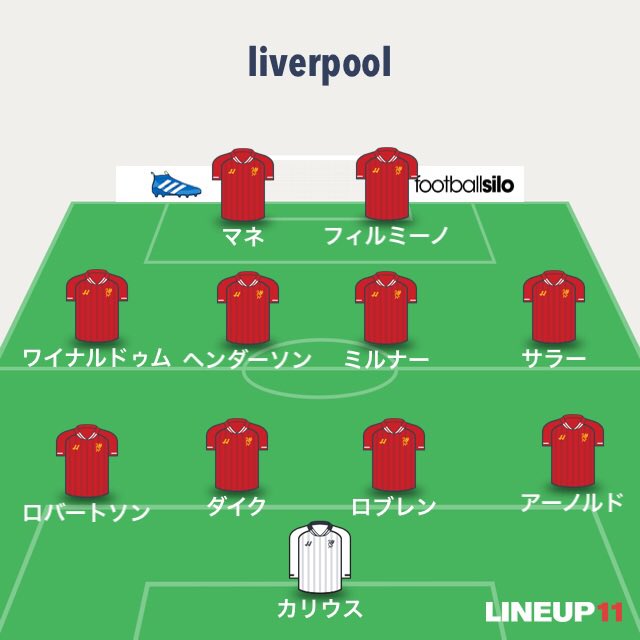
だけど、この様に3-3-3-1で組めば23辺、つまり四角形が4つと1トップによる三角形で辺（パスコース）が増える。

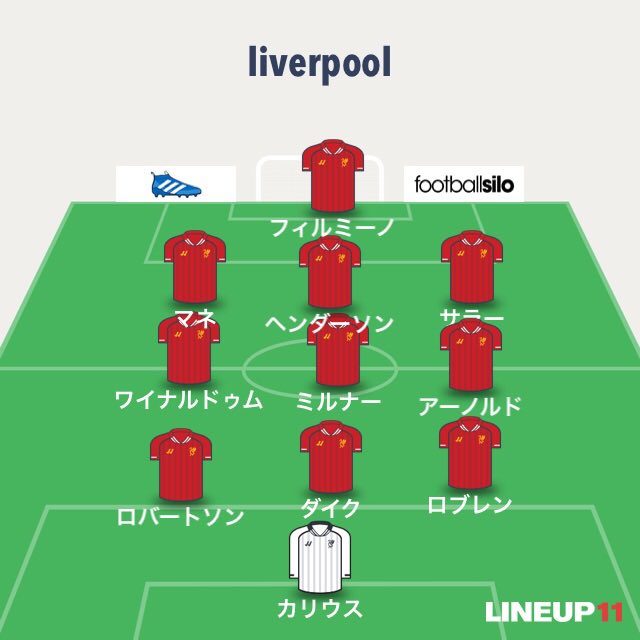
選手間の距離を均等に、かつパスコースを増やし、その上でピッチ全体をカバー出来る事を考えたら、3-3-3-1になるのでは？と考えたのかもしれない。今までの守備戦術というのは相手の攻撃を待ち構えて跳ね返すという事に主眼が置かれていた訳だけど、現代フットボールの戦術は攻守の切り替えでまず相手の攻撃を無効化→出来ない場合は今まで通り守備陣形を組んで防ぐという2段階で組まれてる。これが進化するとどうなるか？

守備陣形を組むというのは1チームが11人である以上、陣形を組む人数を増やすという形以外での発展は難しい。ランチェスターの法則だ。頭数が増えれば戦力（守備陣形の防御能力）は増える。それに対して攻守の切り替えで相手の攻撃を無効化するというのは、言って見れば「ボールが奪われなければ失点しない」という相手の攻撃をゼロにする発想だ。だから、まず奪われないというのが基本コンセプトとなる。そうなれば選手間のパスコースを増やす配置は何か？という考え方になる。

この発想そのものは3-4-3のトータルフットボールが作り上げたモノになると思う。リバプールがクロップのもとでこのまま進化すればトータルフットボールをやる羽目になる書いたのは、この「まず奪われない為にはどうするか？」という問題に直面すると思ったからでもある。

こういった3-4-3だとパスコースは19辺になる。だから3-3-3-1よりもパスコースが少ない。ここから模索したのかもしれない。

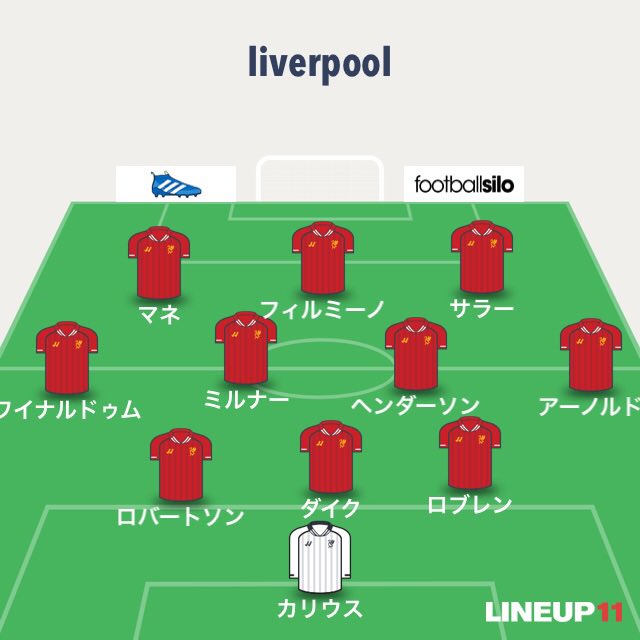
この様な4-2-3-1だと、基本的には19辺。SBと両サイドのアタッカーのパスコースがあると考えても21辺。

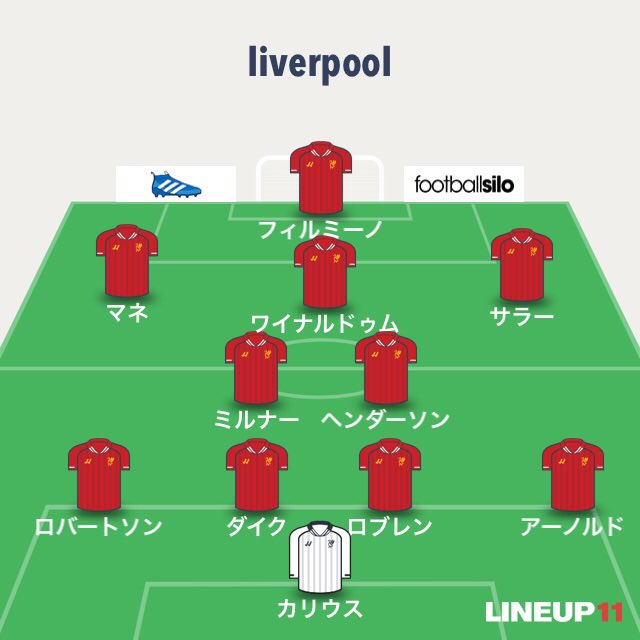
3-3-3-1の話のヒントは恐らくこの記事。記事の中にある「これは、ポルトガルのスポーツ科学者ジャイメ・サンパイオ氏の分析動画の一部を抜粋したものである」から考えてもポルト大の講義が何らかの幾何学的な分野からの影響を受けている可能性は高い。

試合を制する“スペースの支配”を、「幾何学」によって再解釈する／ミランのテクニカルセンターでも活躍するマッシモ・ルッケージは「現代フットボールを分析するために、幾何学は重要な枠組みになりつつある」と述べている。今https://t.co/7iE9ifQlgu pic.twitter.com/FnFzKwzpSp

— footballista (@footballista_jp) 2018年3月19日

幾何学というと難しい話になりそうだけど、シンプルに考えればボールを自分達が支配してるスペースに運び続ける為には正確に支配してるスペースを割り出す必要がある→幾何学の分野だね。って事だと思う。その上で人は運動能力とは別に予測能力で支配するスペースを増やす事が出来る。

同じくfootballistaのこの記事にある様に、シャビやピルロといった選手は試合展開から各選手が動く事で自分達の支配するスペースがどう変化するかを直感的に予測している。なので、彼等の様な選手を有するチームは選手が移動して支配するスペース以上の支配領域を確保できる。

【NEW】なぜ「認知」は重要なのか？スポーツ的「直感」の磨き方https://t.co/74oYyKSle6
――日本人のサッカー選手がプレーする際、脳の前頭前野が活動し、文字通り「考えて」プレーしているのに対して、シャビの場合は大脳基底核が活動している。この部位は「直感」が働く際に活動する場所である

— footballista (@footballista_jp) 2018年3月14日

この「自分達の支配するスペースの予測」をピルロやシャビの様な天才に頼らずに行おうとする場合、最も広く支配領域を確保しようとすると選手間の距離や位置をできる限り均等に配置しようとする形になるだろう。大昔、まだ人類が城や砦を支配領域の拠点とした時代がそうだった様に。

Embed from Getty Images

＜了＞